Bentuk Umum dari logaritma adalah sebagai berikut :
Jika dengan
dengan 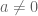 dan
dan  maka
maka 
Grafik fungsi logaritma dibedakan menjadi dua yaitu untuk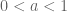 dan untuk
dan untuk 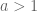
 , untuk
, untuk 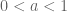
Misalnya salah satu kasus yaitu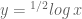
Fungsi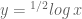 memiliki sifat-sifat:
memiliki sifat-sifat:
terdefinisi untuk semua x > 0;
jika x mendekati nol maka y besar sekali dan bertanda positip;
untuk x = 1, y = 0
untuk x lebih besar dari 1, y berharga negatip. Jika x semakin besar, maka y semakin kecil;
 , untuk
, untuk 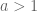
Dipelajari salah satu kasus yaitu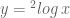
Fungsi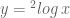 memiliki sifat-sifat:
memiliki sifat-sifat:
terdefinisi untuk semua x > 0;
jika x mendekati nol maka y kecil sekali dan bertanda negatip;
untuk x = 1, y = 0
untuk x lebih besar dari 1, y berharga positip. Jika x semakin besar, maka y semakin besar pula;
Dalam fungsi logaritma dikenal satu fungsi khusus yaitu fungsi logaritma dengan bilangan pokok e, yang disebut logaritma Napier, disingkat ln (dibaca len). Jadi logaritma dengan bilangan pokok e adalah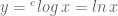
Jika
Grafik fungsi logaritma dibedakan menjadi dua yaitu untuk
Misalnya salah satu kasus yaitu
Fungsi
terdefinisi untuk semua x > 0;
jika x mendekati nol maka y besar sekali dan bertanda positip;
untuk x = 1, y = 0
untuk x lebih besar dari 1, y berharga negatip. Jika x semakin besar, maka y semakin kecil;
Dipelajari salah satu kasus yaitu
Fungsi
terdefinisi untuk semua x > 0;
jika x mendekati nol maka y kecil sekali dan bertanda negatip;
untuk x = 1, y = 0
untuk x lebih besar dari 1, y berharga positip. Jika x semakin besar, maka y semakin besar pula;
Dalam fungsi logaritma dikenal satu fungsi khusus yaitu fungsi logaritma dengan bilangan pokok e, yang disebut logaritma Napier, disingkat ln (dibaca len). Jadi logaritma dengan bilangan pokok e adalah
Tidak ada komentar:
Posting Komentar